Introduction

In this project, we explore two fundamental machine learning techniques: K-Means Clustering and Principal Component Analysis (PCA). These techniques are widely used in image compression, data compression, pattern recognition, and computer vision. Through practical examples, we demonstrate how clustering helps reduce complexity in images and how dimensionality reduction preserves essential features while simplifying data representation.

K-Means Clustering is an unsupervised learning algorithm used to group similar data points into K clusters. K-means clustering is the Process in clustering similar data points in a 2D space into groups and widely used in grouping like:

• ✅ Customers with similar purchasing habits,
• ✅ Geographic locations of different cities,
• ✅ Sensor data from different environmental conditions, etc.

In the context of image processing, we apply K-Means to perform color quantization, reducing the number of colors in an image while maintaining visual integrity.

The goal of K-Means is to minimize the total within-cluster variance, also known as the cost function (J):

\[ J = \sum_{i=1}^{m} \sum_{k=1}^{K} w_{ik} || x_i - C_k ||^2 \]

where:

• \( m \) = number of data points
• \( K \) = number of clusters
• \( x_i \) = data point \( i \)
• \( C_k \) = centroid of cluster \( k \)
• \( w_{ik} \) = 1 if \( x_i \) belongs to cluster \( k \), otherwise 0

Centroid is the center of a cluster. It is an imaginary point that represents the average position of all points in that cluster.

The centroid of a cluster \( k \) is calculated as the mean of all points \( x_i \) in that cluster:

\[ C_k = \frac{1}{N_k} \sum_{i=1}^{N_k} x_i \]

where:

• \( C_k \) = centroid of cluster \( k \)
• \( N_k \) = number of points in cluster \( k \)
• \( x_i \) = data points in cluster \( k \)

2️⃣ Principal Component Analysis (PCA)

Principal Component Analysis (PCA) is a powerful dimensionality reduction technique that finds the most important features in high-dimensional data. PCA is particularly useful in face recognition, where we extract key facial features to represent images efficiently.

How We Proceed

✅ Clustering datasets (K-Means for clustered data)

✅ Bird Image (K-Means for Image Compression)

• The original bird image contains millions of colors in RGB format.
• We apply K-Means clustering to reduce the image to only K colors.
• This technique helps in image compression while preserving quality.

✅ Face Image (PCA for Dimensionality Reduction)

• A grayscale face image consists of thousands of pixels, making it high-dimensional.
• We use PCA to extract the most important features (principal components).
• This reduces storage size and improves efficiency in face recognition.

Project Goals

• 📌 Demonstrate K-Means Clustering using a bird image for color quantization.
• 📌 Apply PCA on face images to reduce dimensions while preserving essential features.
• 📌 Visualize results using side-by-side comparisons of the original and processed images.

Through these examples, we highlight the power of unsupervised learning techniques in image processing and data compression. Let’s dive in! 🚀

1. Setup libraries

1.1 Importing Required Libraries:

        
            Python:

            import imageio.v2 as imageio
            import matplotlib.pyplot as plt
            import numpy as np
            from random import sample #Used for random initialization
        
    

Exppanation:

• numpy is used for numerical operations, especially handling matrices and arrays.
• matplotlib.pyplot is used for visualization.
• random.sample helps in randomly selecting data points for initialization.

1.2 Function to Compute Squared Distance

        
            Python:

            def distSquared(point1, point2):
                assert point1.shape == point2.shape
                return np.sum(np.square(point2 - point1))
        
    

Explanation

• This function def distSquared(point1, point2) computes the squared Euclidean distance between two points.
• It first checks that the two points have the same shape.
• It calculates the squared difference for each dimension and sums them up.
• The squared distance is used instead of the actual Euclidean distance to avoid unnecessary square root calculations, which speeds up the process.

1.3 Finding Closest Centroids

Python codes:

        
            Python:

            def findClosestCentroids(myX, mycentroids):
                idxs = np.zeros((myX.shape[0], 1))
            
                for x in range(idxs.shape[0]):
                    mypoint = myX[x]
                    mindist, idx = 9999999, 0  # Initialize with a large number
                
                    for i in range(mycentroids.shape[0]):
                        mycentroid = mycentroids[i]
                        distsquared = distSquared(mycentroid, mypoint)
                    
                        if distsquared < mindist:
                            mindist = distsquared
                            idx = i
                
                    idxs[x] = idx  # Assign closest centroid index
            
                return idxs
        
    

Code Explanation

• The function def findClosestCentroids(myX, mycentroids) assigns each data point in X to the nearest centroid.
• It initializes an array idxs to store the index of the closest centroid for each data point.
• For each point in X:
  1. It compares the squared distance to each centroid.
  2. The centroid with the smallest distance is assigned as the closest centroid.
• The function returns a (m,1) vector where each element represents the assigned cluster for a point in X.

1.4 Assigning Data Points to Clusters

        
            Python:

                idxs = findClosestCentroids(X, initial_centroids)
                print(idxs[:3].flatten())  # Print the first 3 cluster assignments

                Output:
                    [0. 2. 1.]
        
    

Explanation:

• The function findClosestCentroids is called with X (data points) and initial_centroids (three predefined centroids).
• It returns a list where each data point is assigned a cluster (0, 1, or 2).
• The first three data points are assigned to clusters 0, 2, and 1, respectively.
• This means:
  1. The first data point is closest to centroid 0 (first centroid in initial_centroids).
  2. The second data point is closest to centroid 2.
  3. The third data point is closest to centroid 1.

1.5 Computing New Centroid Positions

        
            Python:

                def computeCentroids(myX, myidxs):
                    """
                    Function takes in the X matrix and the index vector
                    and computes a new centroid matrix.
                    """
                    subX = []
                    for x in range(len(np.unique(myidxs))):
                        subX.append(np.array([myX[i] for i in range(myX.shape[0]) if myidxs[i] == x]))
                
                    return np.array([np.mean(thisX,axis=0) for thisX in subX])
        
    

Function Breakdown:

• The function def computeCentroids(myX, myidxs) computes the new centroid positions after assigning data points to clusters.
• Inputs:
  1. myX: The dataset (each row is a data point).
  2. myidxs: The cluster assignments for each point (from findClosestCentroids).
• Steps:
  1. The function first groups data points by their assigned cluster.
  2. For each cluster, it calculates the mean of all assigned points.
  3. The new centroids are returned as an array.

Why is this Needed?

• After assigning points to clusters, we must update the centroids based on the average position of points in each cluster.
• These updated centroids are used in the next iteration of K-means.

1.6 Finding Closest Centroids

Python codes:

        
            Python:

                def runKMeans(myX, initial_centroids, K, n_iter):
                    """
                    Function that actually does the iterations
                    """
                    centroid_history = []
                    current_centroids = initial_centroids
                
                    for myiter in range(n_iter):
                        centroid_history.append(current_centroids)
                        idxs = findClosestCentroids(myX, current_centroids)
                        current_centroids = computeCentroids(myX, idxs)
                    
                    return idxs, centroid_history

        
    

Function Breakdown:

• The function def runKMeans(myX, initial_centroids, K, n_iter) implements the iterative K-means clustering process.
• Inputs:
  1. myX: The dataset.
  2. initial_centroids: Initial centroid positions.
  3. K: Number of clusters.
  4. n_iter: Number of iterations for K-means.
• Steps:
  1. It stores the centroid positions after each iteration in centroid_history.
  2. For each iteration:
     • Assigns points to the nearest centroid (findClosestCentroids).
     • Computes new centroid positions (computeCentroids).
• Returns the final cluster assignments and the history of centroid positions.

Why is this Needed?

• K-means is an iterative algorithm, meaning it refines centroids over multiple steps until convergence.
• The centroid_history allows visualization of centroid movement.

1.7 How Initial Centroids Affect K-Means Clustering Visualizations?

1.7.1 Choosing Random Initial Centroids

        
            Python:

                def chooseKRandomCentroids(myX, K):
                    rand_indices = sample(range(0,myX.shape[0]),K)
                    return np.array([myX[i] for i in rand_indices])    
        
    

Explanation

• The function def chooseKRandomCentroids(myX, K) selects K random points from the dataset X to use as initial centroids for K-Means clustering.
• sample(range(0,myX.shape[0]),K) randomly selects K unique indices from the dataset.
• The function then returns the corresponding K points from X as initial centroids.

🛠 Why is this needed?

• K-Means clustering is sensitive to initialization. Different initial centroids can lead to different clustering results.
• This function helps ensure that the centroids are randomly selected, reducing bias in clustering.

2. Image Compression with K-Means

2.1 Understanding the Alpha Channel and Why We Remove It Before Image Compression

An alpha channel is an additional layer in an image that controls transparency. It is mainly used in RGBA images, where:

• R (Red)
• G (Green)
• B (Blue)
• A (Alpha) → Controls transparency

A fully opaque pixel has an alpha value of 255, while a fully transparent pixel has an alpha value of 0.

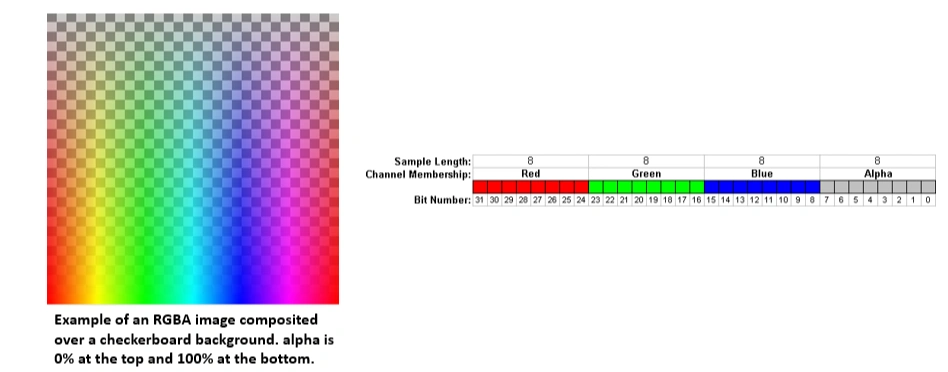
Image 3: K-means Clustering graph 3 with different initial Centroids

Why Remove the Alpha Channel Before Image Compression?

When performing K-Means clustering for image compression, removing the alpha channel is necessary due to the following reasons:

1️⃣ K-Means Clustering Works on RGB Colors

- The clustering algorithm groups colors (R, G, B), not transparency levels.

- If the alpha channel is included, K-Means would treat transparent and opaque pixels as different colors, leading to inaccurate clustering.

2️⃣ Prevents Errors in Image Processing

- Many image processing functions expect a 3-channel (RGB) image and do not support 4-channel (RGBA) images.

- Including the alpha channel may cause errors or unexpected results.

3️⃣ Ensures Consistent Image Representation

- Removing the alpha channel ensures that all pixels have the same structure (R, G, B values only).

- This simplifies reshaping and processing the image for compression.

How Do We Remove the Alpha Channel?

In our code, we check if the image has an alpha channel and remove it:

                        # Check if the image has an alpha channel (RGBA format)
                        if A.shape[2] == 4:  
                            A = A[:, :, :3]  # Keep only the first three channels (RGB)
                    

✅ This keeps only the first 3 channels (R, G, B) and discards transparency.

When is the Alpha Channel Needed?

While removing the alpha channel is essential for K-Means clustering, it is useful in other cases like:

• Transparent logos or overlays
• Web design with semi-transparent elements
• Layered images in graphic design software

For image compression, removing the alpha channel helps produce a clean and accurate color clustering.

2.2 K-means on pixels:

This part of the project applies K-Means clustering to an image to perform image compression by reducing the number of unique colors in the image.

Python codes:

        
            # Load image
            datafile = r'd:\mysite\images\red_birds2.png'
            A = imageio.imread(datafile)

            # Check if image has 4 channels (RGBA), convert to RGB
            if A.shape[2] == 4:  # Check if there's an alpha channel
                A = A[:, :, :3]  # Keep only the first three channels (RGB)

            # Display shape and image
            print("A shape after removing alpha channel:", A.shape)
            plt.imshow(A)
            plt.axis("off")  # Hide axes
            plt.show()

            A = A / 255.0     # Normalize pixel values (0 to 1)
            A = A.reshape(-1, 3) # Reshape image to (num_pixels, 3)
            print("New A shape:", A.shape)

            # Run k-means clustering
            myK = 16
            idxs, centroid_history = runKMeans(A, chooseKRandomCentroids(A, myK), myK, n_iter=10)       
        
    

Comments:

In the codes by myK = 16, we explicitly set 16 centroids enabling to store 16 colors in the future.

Output:

Image 4: Bird image for compression after removing alpha channel

The output indicates that now the image is of (348, 271, 3), which means image is:

• 348 pixels in height
• 271 ixels in width
• 3 channels (RGB)
• 4th channel Alpha is removed

At the bottom of output image "New A shape: (94308, 3)" indicates that:

• Image is reshaped to → (348 x 271, 3) = (94308, 3)
• 94308 → total number of pixels in the image
• 3 → Each pixel has 3 values (RGB = Red, Green, Blue)

Assigning Each Pixel to the Closest Centroid

        
            Python:

                idxs = findClosestCentroids(A, centroid_history[-1])
        
    

What this does:

• The findClosestCentroids function assigns each pixel to its nearest centroid (one of the 16 colors).
• centroid_history[-1] contains the final centroid positions after 10 iterations of K-Means.
• idxs stores the index of the closest centroid for each pixel in the reshaped image.

✅ At this point, each pixel is mapped to one of the 16 colors from K-Means clustering.

Reconstructing the Image with 16 Colors

        
            final_centroids = centroid_history[-1]
            
            final_image = np.zeros((idxs.shape[0], 3))  # Create new image with only 16 colors

            for x in range(final_image.shape[0]):
                final_image[x] = final_centroids[int(idxs[x].item())]  # ✅ Use .item() to extract scalar
        
    

What this does:

• final_centroids = centroid_history[-1] → Stores the final 16 centroid colors.
• final_image = np.zeros((idxs.shape[0], 3)) → Creates an empty array for the compressed image.
• The loop assigns each pixel in the final_image to the corresponding centroid color.

✅ At this point, the image is reconstructed using only 16 unique colors instead of the original full-color spectrum.

Displaying the Images

        
            orig_height, orig_width = 348, 271  # Use the correct values  
                # Get the original image dimensions
            plt.figure()  # Reshape the original and compressed images correctly
            dummy = plt.imshow(A.reshape(orig_height, orig_width, 3))  # ✅ Correct shape
            plt.figure()
            dummy = plt.imshow(final_image.reshape(orig_height, orig_width, 3))  # ✅ Correct shape
            plt.show()
        
    

What this does:

• First plt.figure() and plt.imshow(A.reshape(orig_height, orig_width, 3))
  → Displays the original image before compression.
• Second plt.figure() and plt.imshow(final_image.reshape(orig_height, orig_width, 3))
  → Displays the compressed image with 16 colors.
• plt.show() → Renders both images.

✅ At this point, two images are displayed as output:

• Original image
• Compressed image using only 16 colors

Image 5: Comparison between original and compressed image.

Observations

While compression significantly reduces the number of unique colors in the image, it does not degrade the overall quality. Instead, it enhances the separation of different regions, making boundaries between colors more visible.

Key Takeaways:

1. Dimensionality Reduction with PCA

- PCA was applied to image data, starting with feature normalization and computing Singular Value Decomposition (SVD) to extract principal components.
- This helped project high-dimensional image data into lower-dimensional spaces while retaining important features.

2. Eigenfaces and Face Representation

- By extracting eigenfaces from a dataset of human faces, we visualized the most significant facial features.
- Reducing image dimensions allowed us to compress and reconstruct faces while analyzing how much detail was preserved.

3. Image Compression & Reconstruction

- Images were projected onto a lower-dimensional subspace (e.g., 36 principal components) and reconstructed to evaluate the loss of detail.
- The reconstructed images retained main features, demonstrating PCA’s effectiveness in image compression.

4. Color Clustering & PCA Visualization

- PCA was used to reduce RGB color data from 3D to 2D for easier visualization of color clusters.
- The final PCA projection plot illustrated how PCA can assist in image segmentation and clustering.

Final Thoughts

This project successfully demonstrated PCA’s power in reducing data complexity while maintaining essential structure in images. From face recognition to color compression, PCA proves to be a valuable tool in machine learning and computer vision.

Future improvements could involve exploring non-linear dimensionality reduction techniques like t-SNE or Autoencoders for better visualization and reconstruction quality.

🚀 Thank you for following along!