Introduction

Advanced SVM Techniques for Machine Learning

Support Vector Machines (SVM) are among the most powerful and widely used machine learning algorithms for classification tasks. This project explores the implementation of SVM with different kernel functions and applies hyperparameter tuning to applied various SVM configurations, and tested our model's ability to accurately classify data points. Through rigorous experimentation with Gaussian (RBF) kernels, we identified the optimal hyperparameters to enhance decision boundary precision. By the end of this project, we have developed a robust SVM model capable of handling complex, non-linearly separable datasets, making it a valuable tool for real-world applications in pattern recognition, bioinformatics, and image classification.

1. Importing Required Libraries:

        
        Python:

            %matplotlib inline
            import numpy as np
            import matplotlib.pyplot as plt
            import scipy.io #Used to load the OCTAVE *.mat files
            import scipy.optimize #fmin_cg to train the linear regression

            import warnings
            warnings.filterwarnings('ignore')
        
    

• %matplotlib inline ensures that graphs are displayed directly inside the Jupyter Notebook.
• numpy is imported as np for numerical computations.
• matplotlib.pyplot is imported as plt for data visualization.
• scipy.io is used to load MATLAB .mat files, which contain the dataset.
• scipy.optimize provides optimization functions for training models.
• warnings.filterwarnings('ignore') suppresses warning messages for a cleaner output.

2. Loading and Preparing the Dataset

        
            datafile = r'd:\mlprojects\data\ex5data1.mat'
            mat = scipy.io.loadmat(datafile)
            
            # Training set
            X, y = mat['X'], mat['y']
            
            # Cross-validation set
            Xval, yval = mat['Xval'], mat['yval']
            
            # Test set
            Xtest, ytest = mat['Xtest'], mat['ytest']
            
            # Insert a column of 1's to all of the X's, as usual
            X = np.insert(X, 0, 1, axis=1)
            Xval = np.insert(Xval, 0, 1, axis=1)
            Xtest = np.insert(Xtest, 0, 1, axis=1)  datafile = r'd:\mlprojects\data\ex6data1.mat'
            mat = scipy.io.loadmat( datafile )
            #Training set
            X, y = mat['X'], mat['y']
            #NOT inserting a column of 1's in case SVM software does it for me automatically...
            #X =     np.insert(X    ,0,1,axis=1)
            
            #Divide the sample into two: ones with positive classification, one with null classification
            pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
            neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])     
        
    

• The dataset is loaded from an external .mat file (ex6data1.mat).
• X contains the data with two columns for two types of features.
• y contains the labels (1 for positive class, 0 for negative class).
• The dataset is then split into two groups:
  1. pos: Data points labeled as positive (class 1).
  2. neg: Data points labeled as negative (class 0).

3. Plotting the Dataset

    
        def plotData():
            plt.figure(figsize=(10,6))
            plt.plot(pos[:,0], pos[:,1], 'k+', label='Positive Sample')
            plt.plot(neg[:,0], neg[:,1], 'yo', label='Negative Sample')
            plt.xlabel('Column 1 Variable')
            plt.ylabel('Column 2 Variable')
            plt.title("Data without SVM Decision Boundary")
            plt.legend()
            plt.grid(True)
            plt.show()  # Add this line to force displaying the plot

        plotData()

    Output graph:
    

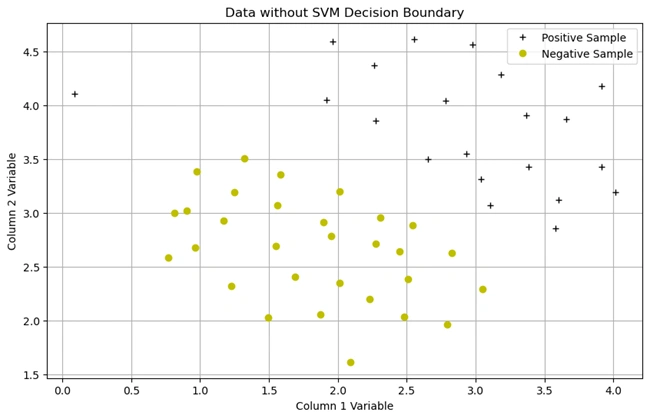
Image 1: Graph without SVM decision boundary

Visualizing the Dataset:

1. Description of the Dataset

• Before applying Support Vector Machines (SVM) for classification, we begin by visualizing the dataset. The dataset consists of two features (X1 and X2), where each point is labeled as either positive (1) or negative (0).
• In the figure above:
  1. Positive samples (black plus +) belong to one class.
  2. Negative samples (yellow circles o) belong to another class.
  3. The points seem clustered into two distinct regions, which indicates that a classification model like SVM can separate them.
• This visualization helps in understanding how SVM will later draw a decision boundary to separate the two classes.
• A grid is added for better readability.

1. Importing Necessary Libraries

        
            Python:

            import numpy as np
            import matplotlib.pyplot as plt
                             
    

• numpy for numerical computations.
• matplotlib.pyplot for plotting graphs.

2. Plotting the Dataset

Python codes:

    
        def plotData():
            # Convert y to a 1D array if it's a column vector
            y_flat = y.ravel()  # Converts (m,1) to (m,)
            
            plt.scatter(X[y_flat == 1][:, 0], X[y_flat == 1][:, 1], marker='+', color='k', label="Positive")
            plt.scatter(X[y_flat == 0][:, 0], X[y_flat == 0][:, 1], marker='o', color='y', label="Negative")

        def plotBoundary(my_svm, xmin, xmax, ymin, ymax):
            xvals = np.linspace(xmin, xmax, 100)
            yvals = np.linspace(ymin, ymax, 100)
            u, v = np.meshgrid(xvals, yvals)  # Create grid
            grid_points = np.c_[u.ravel(), v.ravel()]  # Flatten and merge into (N,2) array
            
            zvals = my_svm.predict(grid_points)  # Predict all at once
            zvals = zvals.reshape(u.shape)  # Reshape back to grid shape
            
            plt.contour(xvals, yvals, zvals, levels=[0], colors='b')  # Overlay decision boundary

        # ✅ Ensure everything is plotted on the same figure
        plt.figure(figsize=(8,6))  # Create a new figure
        plotData()  # Plot scatter data
        plotBoundary(linear_svm, 0, 4.5, 1.5, 5)  # Overlay decision boundary

        # ✅ Add labels and legend
        plt.xlabel("Feature 1")
        plt.ylabel("Feature 2")
        plt.title("SVM Decision Boundary with Data")
        plt.legend()

        plt.show(); # semi-colon (;) used to Suppresses unwanted EXTRA text outputs in J Notebook

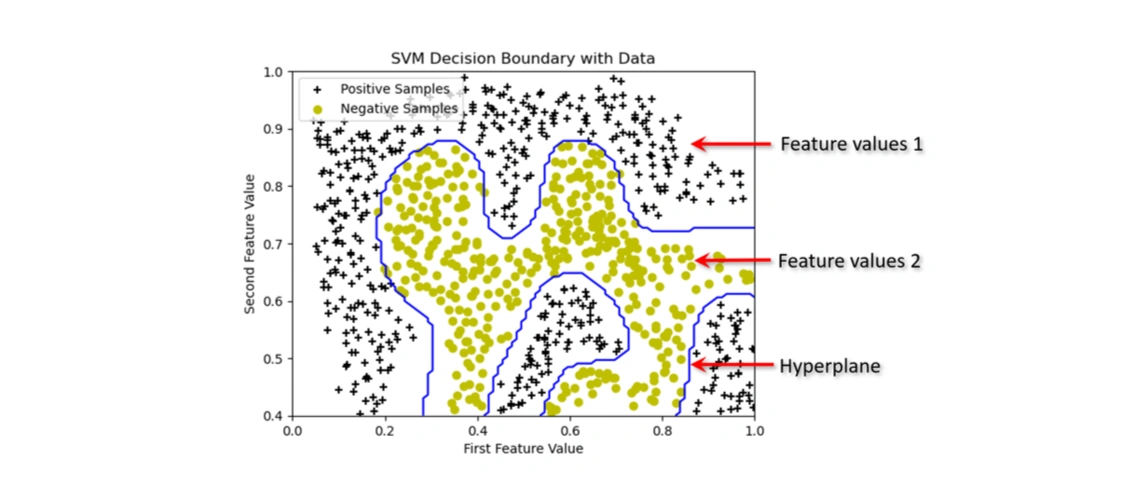
        Output Graph with svm decision boundary
    

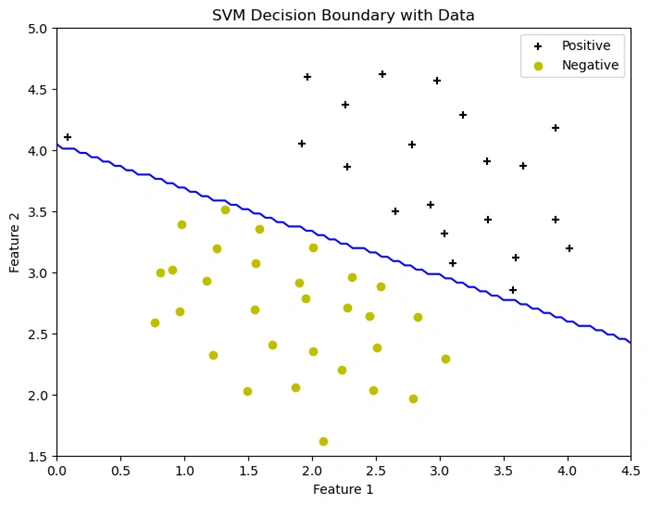
Image 2: Graph with SVM decision boundary

Explanation:

• def plotData() function plots the dataset just like in the previous cell, but now using plt.scatter().
• Black plus signs ('+') for positive samples (y == 1).
• Yellow circles ('o') for negative samples (y == 0).
• y.ravel() ensures y is a 1D array instead of a column vector to avoid indexing issues.
• A grid of points (u, v) is created over the plot area.
• Each point in the grid is classified by the SVM model (my_svm.predict())
• The decision boundary (blue line) is plotted using plt.contour() at z = 0, which represents the SVM's classification boundary.
• Calls plotData() to plot the dataset.
• Calls plotBoundary() to overlay the SVM decision boundary (linear_svm is the trained SVM model).
• plt.show(); ensures the graph is displayed.

3. Important Observation of blue SVM decision boundary line:

• The blue decision boundary separates the positive (black +) and negative (yellow o) samples. However, instead of running perfectly down the middle, the boundary is slightly tilted:
  1. The left end leans towards the negative samples.
  2. The right end leans towards the positive samples.
• This behavior occurs because SVM aims to maximize the margin between support vectors, meaning it prioritizes points closest to the boundary rather than the overall dataset distribution.

In the next step, we will analyze the effect of different kernel functions on the decision boundary.

The Gaussian kernel formula is:

$$ K(x_1, x_2) = \exp\left( \frac{-\|x_1 - x_2\|^2}{2\sigma^2} \right) $$

Where:

• \( K(x_1, x_2) \) is the kernel function that computes the similarity between \( x_1 \) and \( x_2 \).
• \( \|x_1 - x_2\|^2 \) represents the Squared Euclidean Distance between the two feature vectors.
• σ is the kernel bandwidth parameter, controlling how far points influence each other.
• exp(⋅) is the exponential function.

What is Euclidean distance?

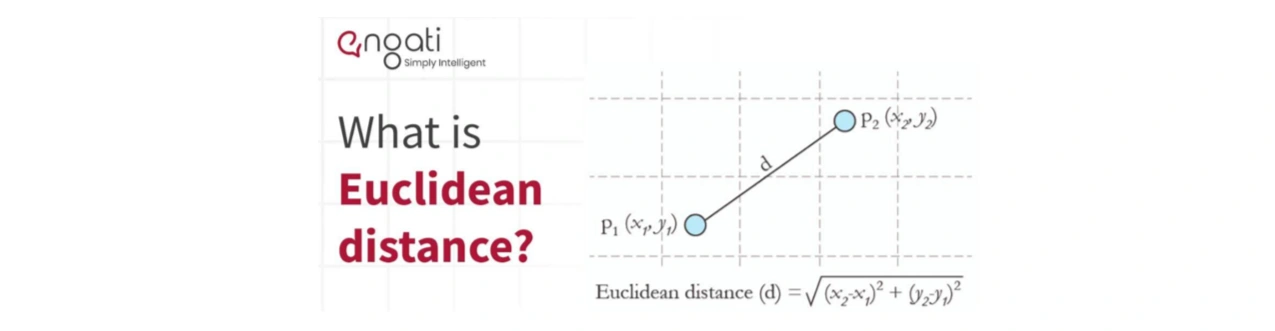
Image 3: Euclidean distance curtesy by www.engati.com

Euclidean distance examines the root of square distances between the co-ordinates of a pair of objects. To derive the Euclidean distance, we would have to compute the square root of the sum of the squares of the differences between corresponding values. Squared Euclidean Distance can be written as \( \|x_1 - x_2\|^2 \).

Code breakdown

Python:

    def gaussKernel(x1, x2, sigma):
        sigmasquared = np.power(sigma,2)
        return np.exp(-(x1-x2).T.dot(x1-x2)/(2*sigmasquared))
    
    print(gaussKernel(np.array([1, 2, 1]),np.array([0, 4, -1]), 2.))
    
    Output:
    0.32465246735834974

• The function computes the similarity between two feature vectors [1, 2, 1] and [0, 4, -1] using sigma = 2.
• Expected output: 0.324652, meaning the two vectors have moderate similarity under this Gaussian kernel.

Python:

    datafile = r'd:\mlprojects\data\ex6data2.mat'
    mat = scipy.io.loadmat( datafile )
    #Training set
    X, y = mat['X'], mat['y']
    
    #Divide the sample into two: ones with positive classification, one with null classification
    pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
    neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])
    
    def plotData():
        plt.scatter(pos[:, 0], pos[:, 1], marker='+', color='k', label="Positive Samples")
        plt.scatter(neg[:, 0], neg[:, 1], marker='o', color='y', label="Negative Samples")
    
    plotData()
    plt.xlabel("First Feature Value")  # Generic label, update if needed
    plt.ylabel("Second Feature Value")  # Generic label, update if needed
    plt.title("Data without SVM Decision Boundary")
    plt.legend()  # ✅ Legend should now appear
    plt.show();  

    Output Graph withot svm decision boundary

Visualizing the Dataset Before Applying SVM

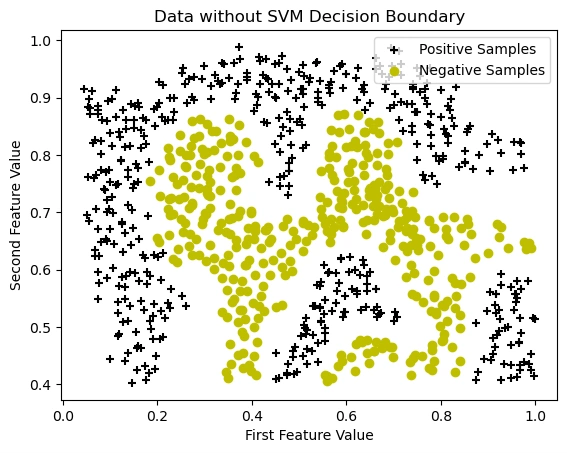
Image 4: Data visualization without SVM decision boundary

• Loads the dataset from the .mat file.
• X contains feature values.
• y contains labels (1 for positive, 0 for negative).

            
                Python:

                pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
                neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])
            
        

• Positive Samples ,(y == 1) are stored in pos
• Negative Samples (y == 0) are stored in neg.
• The above graph shows the raw dataset before training a Support Vector Machine (SVM). The dataset contains two classes:
  1. Positive samples (+, black).
  2. Negative samples (o, yellow).

The data is not linearly separable, meaning a straight-line decision boundary will not work well. This suggests that using an SVM with a Gaussian kernel will be necessary to find a non-linear boundary that accurately separates the two classes.

In the next step, we will train an SVM with a Gaussian kernel and visualize the decision boundary.

Python:

    
        # Train the SVM with the Gaussian kernel on this dataset.
        sigma = 0.1
        gamma = np.power(sigma,-2.)
        gaus_svm = svm.SVC(C=1, kernel='rbf', gamma=gamma)
        gaus_svm.fit( X, y.flatten() )
        plotData()
        plotBoundary(gaus_svm,0,1,.4,1.0)

        plt.xlabel("First Feature Value")  # Generic label, update if needed
        plt.ylabel("Second Feature Value")  # Generic label, update if needed
        plt.title("SVM Decision Boundary with Data")
        plt.legend()  # ✅ Legend should now appear
        plt.show();


        Output Graph with svm decision boundary
    

Visualizing the Dataset After Applying SVM with an RBF (Gaussian) Kernel

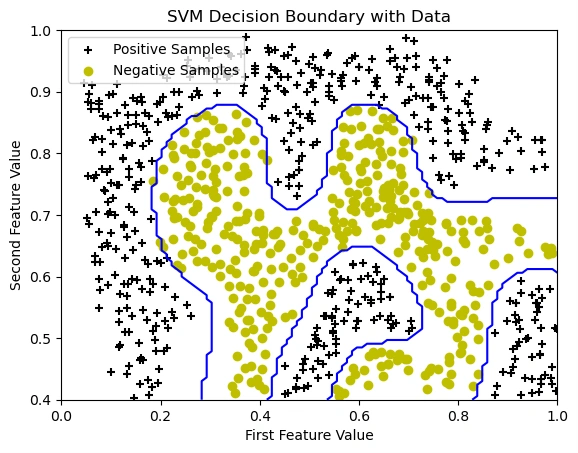
Image 5: The graph showing the data points with the SVM decision boundary.

SVM Decision Boundary Using Gaussian Kernel:

In this step, we trained an SVM classifier using the Radial Basis Function (RBF) kernel to classify data points. Unlike linear SVMs, the RBF kernel enables the decision boundary to be non-linear, adapting to complex data distributions.

The blue curve in the graph represents the decision boundary, which separates the positive (black + markers) and negative (yellow o markers) samples.

We used sigma = 0.1, which determines how tightly the boundary follows the data distribution. The parameter C=1 controls the trade-off between maximizing the margin and minimizing misclassification errors.

As a result, the decision boundary is curved, demonstrating the power of kernel-based SVMs in handling non-linearly separable data.

Observations:

• The blue decision boundary curves to best separate the two classes.
• The shape of the boundary is influenced by sigma and C values.
• The boundary adapts to the data distribution, unlike a linear SVM.

Python:

        
            datafile = r'd:\mlprojects\data\ex6data3.mat'
            mat = scipy.io.loadmat( datafile )
            #Training set
            X, y = mat['X'], mat['y']
            Xval, yval = mat['Xval'], mat['yval']

            #Divide the sample into two: ones with positive classification, one with null classification
            pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
            neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])

            def plotData():
                plt.scatter(pos[:, 0], pos[:, 1], marker='+', color='k', label="Positive Samples")
                plt.scatter(neg[:, 0], neg[:, 1], marker='o', color='y', label="Negative Samples")

            plt.xlabel("First Feature Value")  # Generic label, update if needed
            plt.ylabel("Second Feature Value")  # Generic label, update if needed
            plt.title("Data without SVM Decision Boundary")
            plotData()
            plt.legend()
            plt.show();

            Output Graph without svm decision boundary
        
    

Visualizing the Dataset Before Applying SVM with an RBF (Gaussian) Kernel

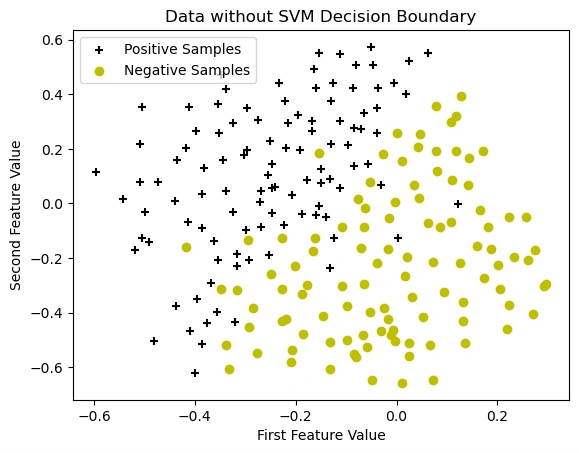
Image 6: The graph showing the data points without SVM decision boundary.

This dataset contains:

• X and y: The training data and corresponding labels.
• Xval and yval: A validation dataset, which is not used in this specific cell but is available for model selection.

    Python:

    X, y = mat['X'], mat['y']
    Xval, yval = mat['Xval'], mat['yval']

    pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
    neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])

• pos: Extracts data points where y == 1 (positive class).
• neg: Extracts data points where y == 0 (negative class).
• This separation helps in plotting the data with different markers/colors.

Plotting the Data

    
        def plotData():
            plt.scatter(pos[:, 0], pos[:, 1], marker='+', color='k', label="Positive Samples")
            plt.scatter(neg[:, 0], neg[:, 1], marker='o', color='y', label="Negative Samples")

        plotData()
    
    

• The function plotData():
  1. Plots positive samples (y=1) using a black plus (+) marker.
  2. Plots negative samples (y=0) using a yellow circle (o) marker
• This visualization helps to observe the distribution of different classes.

Explanation of the Output Graph:

This graph represents the dataset before applying the Support Vector Machine (SVM) model. The data consists of two classes:

• Positive samples (+ black markers)
• Negative samples (o yellow markers)

The purpose of this visualization is to analyze the distribution of the data before training a model. The dataset appears to be non-linearly separable, meaning a simple linear classifier may not perform well.

Next, we will apply an SVM classifier with a Gaussian (RBF) kernel to learn a decision boundary that effectively separates these two classes.

Python:

        
            datafile = r'd:\mlprojects\data\ex6data3.mat'
            mat = scipy.io.loadmat( datafile )
            #Training set
            X, y = mat['X'], mat['y']
            Xval, yval = mat['Xval'], mat['yval']

            #Divide the sample into two: ones with positive classification, one with null classification
            pos = np.array([X[i] for i in range(X.shape[0]) if y[i] == 1])
            neg = np.array([X[i] for i in range(X.shape[0]) if y[i] == 0])

            def plotData():
                plt.scatter(pos[:, 0], pos[:, 1], marker='+', color='k', label="Positive Samples")
                plt.scatter(neg[:, 0], neg[:, 1], marker='o', color='y', label="Negative Samples")

            plt.xlabel("First Feature Value")  # Generic label, update if needed
            plt.ylabel("Second Feature Value")  # Generic label, update if needed
            plt.title("Data without SVM Decision Boundary")
            plotData()
            plt.legend()
            plt.show();

            Output:
            Best C, sigma pair is (0.300000, 0.100000) with a score of 0.965000.
        
    

Output Interpretations:

        
            Python:

            Best C, sigma pair is (0.300000, 0.100000) with a score of 0.965000.
        
    

Setting Up Hyperparameters Values

    Python:

    Cvalues = (0.01, 0.03, 0.1, 0.3, 1., 3., 10., 30.)
    sigmavalues = Cvalues

• Cvalues and sigmavalues are defined as possible values for C (regularization parameter) and σ (RBF kernel parameter).
• These values are commonly used for grid search when tuning SVM hyperparameters.

Initializing Variables for Best Parameters

    Python:

    best_pair, best_score = (0, 0), 0

• best_pair: Stores the best (C, sigma) values.
• best_score: Tracks the highest validation accuracy obtained.

Looping Over All (C, σ) Pairs

    Python:
    
    for Cvalue in Cvalues:
        for sigmavalue in sigmavalues:
            gamma = np.power(sigmavalue,-2.)
            gaus_svm = svm.SVC(C=Cvalue, kernel='rbf', gamma=gamma)
            gaus_svm.fit( X, y.flatten() )
            this_score = gaus_svm.score(Xval,yval)

• Nested loops iterate over all combinations of C and sigma.
• Gamma ( γ ) is calculated as: \[ \gamma = \frac{1}{\sigma^2} \]
• This is how sigma is related to the Gaussian (RBF) kernel in SVM.
• A new SVM model (gaus_svm) is trained with the given C and gamma.
• The accuracy (this_score) is measured using the score() function on the validation set (Xval, yval).

In this step, we used cross-validation to find the optimal values of C (regularization parameter) and σ (RBF kernel parameter) for our Support Vector Machine (SVM) model.

We conducted a grid search over predefined values of C and σ to identify the best-performing combination. The model was trained multiple times with different parameters, and the accuracy was evaluated using the validation set.

Best Parameters Found:

• C = 0.3
• σ = 0.1
• Validation Accuracy: 96.5%

This tuning ensures that the SVM model generalizes well to new, unseen data, avoiding underfitting or overfitting.

    
        Python:

            gaus_svm = svm.SVC(C=best_pair[0], kernel='rbf', gamma = np.power(best_pair[1],-2.))
            gaus_svm.fit( X, y.flatten() )
            plotData()
            plotBoundary(gaus_svm,-.5,.3,-.8,.6)
            plt.xlabel("First Feature Value")  # Generic label, update if needed
            plt.ylabel("Second Feature Value")  # Generic label, update if needed
            plt.title("SVM Decision Boundary with Data")
            plt.legend()
            plt.show();
    

Output graph with SVM decision boundary

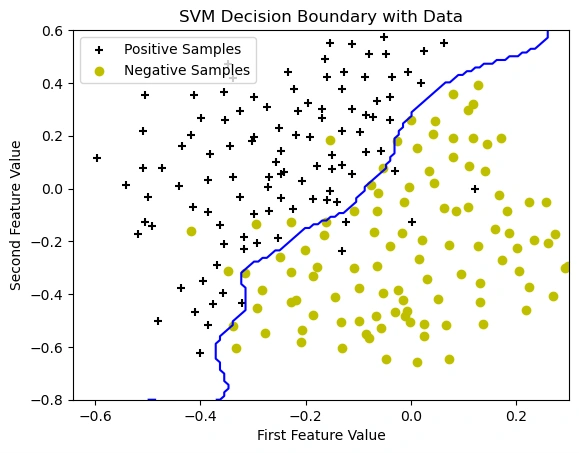
Image 7: The graph showing the data points with SVM decision boundary.

Interpretations of the graph:

In this step, we trained an SVM model with the best hyperparameters and plotted the decision boundary. The Gaussian (RBF) kernel allows the model to learn a complex, non-linear boundary that effectively separates the positive and negative classes.

🔹 Observations from the graph:

• The zigzag pattern of the decision boundary indicates that the SVM model is highly sensitive to small changes in data.
• This is a result of using a Gaussian (RBF) kernel, which allows the boundary to be non-linear and flexible.
• The SVM model correctly classifies most data points while avoiding overfitting.
• The support vectors influence the placement of the boundary.
• This approach ensures that our SVM classifier generalizes well to unseen data, making it a powerful model for non-linearly separable datasets.

Acknowledgments

I sincerely thank Prof. Andrew NG (DeepLearning.AI, Stanford University) for his inspiring courses that laid the foundation for this project.